The Roche Limit is a useful concept to learn about when trying to understand the ring systems around the giant planets Saturn, Uranus and Neptune. (Jupiter's ring system is strange, we will talk about that in lecture). The Roche Limit was first described by the French mathematician Edouard Albert Roche (1820 - 1883) in 1848. The simplest definition of the Roche Limit is that it is the closest distance a body held together by self-gravity can come to a planet without being pulled apart by the planet's tidal (gravity) force. What does this mean?
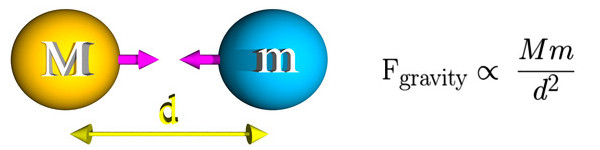
In the Gravity tutorial, we learned about the force of gravity by imagining a universe consisting only of two spherical objects with masses M and m. These masses are separated by a distance d (the distance is measured from the center-of-mass of the spheres). We found that the force of gravity attracting the two sphere together, can be express by the, now familiar, formula shown on the right. The important thing to notice in this tutorial, is that force is very strongly dependent on the distance between the objects.

Now let us make the problem a little more interesting by placing the two masses (red and blue) in the vicinity of a very large mass (yellow). The red and blue masses are still attracted together by the force of gravity. However, they are also attracted to the large yellow mass.
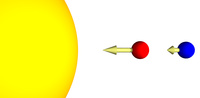
Remember that the force of gravity is is very strongly dependent on the distance between the objects. Since the red mass is closer to the large yellow mass, it feels a slightly larger gravitational force that the blue mass feels.
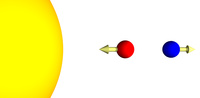
This difference in gravitation forces means that the red mass and the blue mass would tend to move apart. As you can see there are two forces at work on the red and blue masses. The gravitational force between them will attract them together, while the differential gravitational force from the large yellow mass, will separate them.
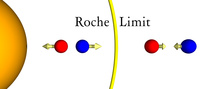
Which of the two forces will dominate depends on the distance the red and blue masses are from the large yellow mass. If the two smaller masses are far away from the large mass, the attractive force is dominate. If the two masses are close to the larger mass the repulsive force will dominate. The border between these two cases is call the Roche Limit
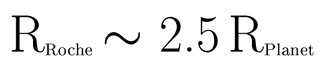
The actual location of the Roche Limit depends on the densities of masses involved. For typical objects that we encounter in Astronomy 150, the location of the Roche Limit is approximately 2.5 times the radius of the central planet. This is measured from the center of the central planet, so it is 1.5 radii from the planet's surface.

So what does all of this have to do with rings? Well, the ring systems of the giant planets all lie within the Roche limits of the planets. The rings are remnants of material of the early solar system that never formed into satellites because they were within the Roche limit. When two object came together, they did not accrete into a larger body, but moved apart and stayed smaller objects. A bit of an oversimplification is: inside Roche limit - Rings, outside Roche limit - satellites.
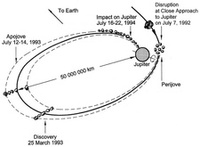
On July 7, 1992, the Comet Shoemaker-Levy 9 broke apart into 21 pieces due to tidal forces when it passed within Jupiter's Roche Limit; on the subsequent pass, each of the comet's pieces collided with Jupiter. The fact that Shoemaker-Levy 9 broke apart within Jupiter's Roche limit tells us that the mechanical strength of the comet's nucleus was not very great. The comet's nucleus was most likely a rubble pile. A rubble pile is a weak aggregate of large and small particles held together by gravity rather than material strength.

This little tutorial is a very qualitative discussion of the Roche Limit. If you want to dive into all of the fun mathematics the Wikipedia entry is a pretty good place to start.