Gravity is one of the four fundamental forces that exist in nature. While it is the weakest of the four forces, it is the dominate force over the large distances in our solar system. Gravity dictates the orbits of the worlds in our solar system, constrains their internal structure, determines their shape, shapes their surfaces and holds-on to their atmospheres. The force of gravity is ubiquitous in Astronomy 150, hardly a lecture will go by without me mentioning it in some form. This little tutorial is my simple attempt to introduce gravity and show how we will use it most often in this class.
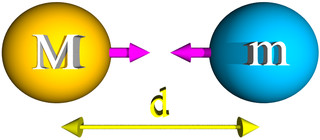
The classic way to introduce gravity is to imagine a universe consisting only of two spherical objects with masses M and m. These masses are separated by a distance d (the distance is measured from the center-of-mass of the spheres).
These two spheres are attracted to each other by the force of gravity. The force of gravity is always attractive (there is no anti-gravity). The force of gravity between two objects (M) and (m) depends of their respective mass and on the inverse of the square of the distance (d) between them. The force is very strongly dependent on the distance between the objects. This strong dependence on distance will be an important property of gravity in Astronomy 150.
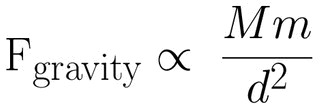
In a more compact form the force of gravity can be expressed by the formula shown on the right. The symbol in the middle that looks like a Greek letter alpha means "proportional to". This formula can be expressed in English to read: "The force of gravity if proportional to the product of the two mass divided by the distance between them squared". Learn this equation! It is really the only formula you will need to know in this class.
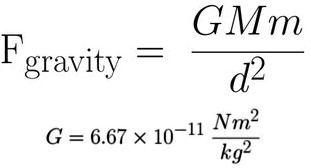
The force of gravity can be more correctly expressed by the equation shown on the left. The only difference between this equation and the formula above is that the "proportional to" has been changed to a "equals to" and a constant G has been added. This constant G is called the universal gravitational constant. G is just a number (shown on the left), so it does not change the relationships in the equation. This is the equation you would use if you wanted to calculated the force of gravity in newtons (or pounds if you used a different value of G). In this class we will mostly use the simpler formulation for gravity shown above.
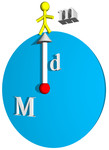
While we will have occasion to talk about two masses separated by a distance in this class, the format we will most often encounter gravity is show in the figure on the right. A person of mass m is standing on a planet of mass M. The person is standing a distance d from the center of the planet. Most often this distance will be the radius of the planet.
You can then calculate the force of gravity between the planet and the person. This calculation is very familiar to us. The force of gravity between you and Earth is called your weight. When you step on the bathroom scale you are measuring the force of gravity between you and Earth.
One interesting consequence of this is that your weight on the Earth depends on the mass of the Earth and the distance between you and the center of the Earth. For example, imagine that you doubled the size of the Earth but keep the mass of the Earth the same (see the figure below). How would your weight change? Well you can determine that by using the formulation shown above and a little algebra.
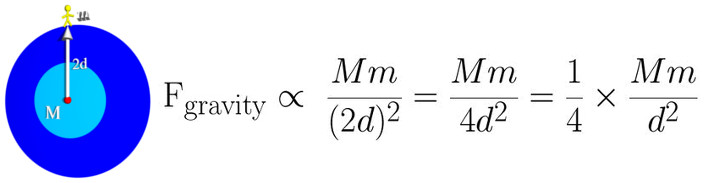
As you can see, increasing your distance from the center of the Earth, decreases your weight. In this case of doubling the Earth's radius, your weight would decrease by a factor of four. For example, a 200 pound person on the normal Earth would weigh 50 pounds on the resized Earth. As an exercise, you should plug other numbers into the gravity equation (especially fractions!) and see how your weight would change.